If there's one thing that is essential to my programming knowledge arsenal, that is the CPU cache. Cache is a double-edged sword that can make the life of a programmer who understands how to deal with it much easier and the life of the one who doesn't extremely more difficult.
Before we discuss cache, we first need to understand RAM (random access memory). RAM is a famous type of memory that is temporary; power off the computer and its contents are lost. We usually think of it as a long array of zeros and ones, but in reality RAM operates quite differently! A better way to think about it is by using a table analogy.
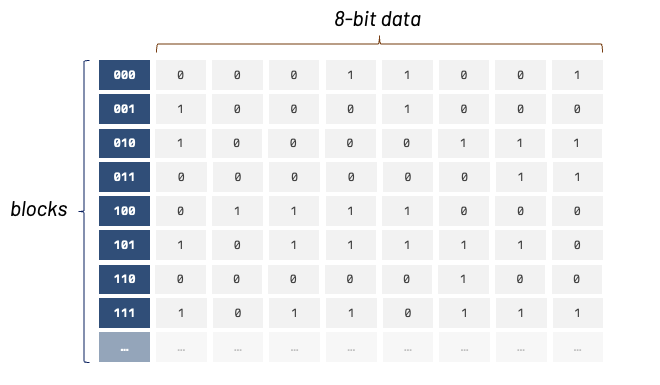
This "table" memory layout makes it easier for the cache to access memory. The cache can load N memory blocks inside. Cache blocks can be of various sizes, and the number of blocks in a cache is usually a power of 2. Common cache line sizes are 32, 64, and 128 bytes.
From now on, we'll refer to these memory blocks as "cache lines." When a cache line is stored into the cache, we also store its memory location.
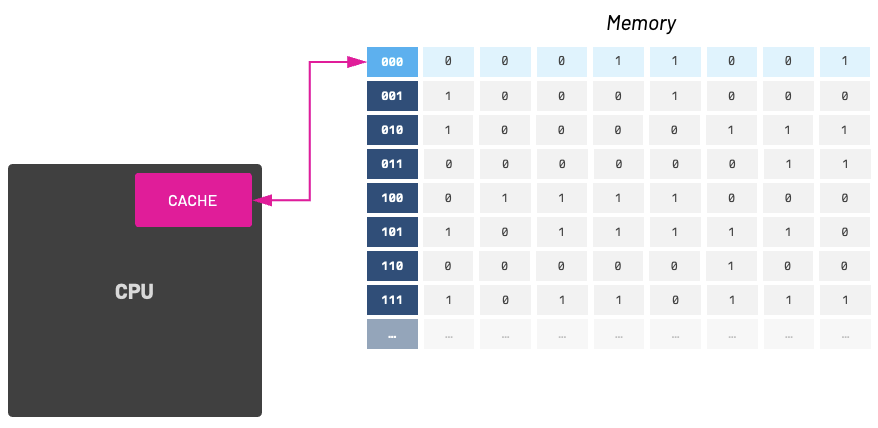
When we successfully store and fetch a cache line we call it a cache hit, otherwise it is a cache miss. As cache-aware programmers, we should try to increase cache hits and avoid cache misses.
Keep in mind that different processor microarchitectures specify different sizes for their cache lines. This cache line size (or cache block size) is the unit of data transferred to and from the main memory. It significantly impacts how effectively the CPU interacts with the memory subsystem. With larger cache lines, you can exploit the spatial locality (proximity) of your data more effectively.
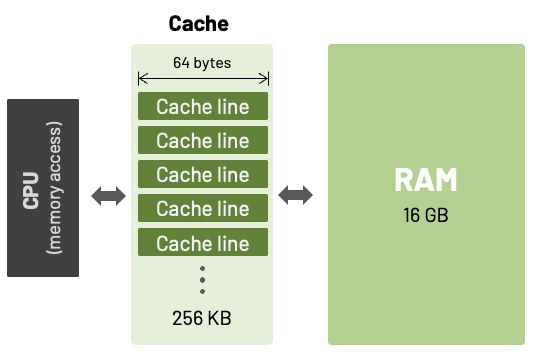
Cache: What is it good for?
The difference of speed between CPU and RAM was minimal in early computers. For example, the early PCs (up to and including 80386) had no cache at all. All memory operations would go from the CPU out to main memory and then back again. As the speed of the CPU increased in comparison to RAM speeds, there was a need to somehow reduce that disparity. The answer was cache memory.
This new approach consisted in a temporary data storage located on the processor, which is used to increase the processing efficiency of the CPU by holding small and often-requested bits of data ready to be accessed at high speed.
Cache is faster than RAM
Since our cache is located inside the CPU, it is much faster for the other parts of the processor to read and write to it.
Most modern CPU cache memory is comprised of different levels of storage. These levels are commonly referred to as L1, L2, L3, and ocasionally L4. They vary in location, speed, and size; most machines have at least 2 levels of cache: L1 and L2.
L1 is low capacity but extremely fast. L2 is slower but has more storage space. L3 is the slowest of the three but also usually has the biggest storage capacity.
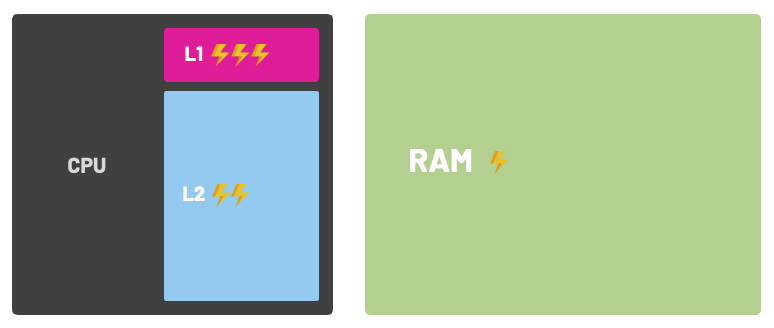
How fast is L1 cache?
When I say L1 is faster, I really mean faster! To put things into perspective, consider that accessing L1 cache can take ~3 CPU cycles, L2 takes ~10 cycles, and normal RAM takes massive ~250 cycles to complete.
You can use tools to inspect the cache sizes of your machine. The image below shows a program called CPU-Z running on an Intel machine with L1, L2, and L3 and different cache line sizes for each level.
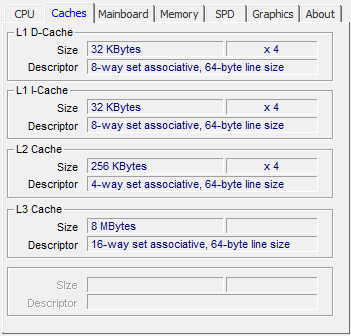
On a macOS system you can use the command-line utility sysctl to view cache information. On Linux, you can inspect your cache sizes with lscpu.
Where is Cache Located?
Starting with the launch of the Intel 486DX in 1989, Intel added a very small cache within the CPU itself. The small cache embedded in the 486 chip was 8 KB in size, and in later generations it would be called "Level 1" cache. As manufacturers started to adopt the 486 CPU, they also began to include a secondary cache on the motherboard. This external cache was called "Level 2" cache and would often use SRAM chips with access times of around 15 or 20 nanoseconds (rather than 70 nanoseconds that was used by normal main memory). Below is an image of the motherboard of a 486SX with two levels of cache: L1 inside the CPU die and L2 cache located externally on the motherboard.

The original Pentium used a split level 1 cache where each level was 8 KB in size; 8 KB for data cache and 8 KB for instruction cache.
The Pentium Pro chip introduced the P6 x86 microarchitecture in 1995 and was famous for having an on board cache. This could be either 256 KB, 512 KB, or 1 MB in size.

More modern architectures are smarter in terms of cache placement and account for multiple CPU cores.
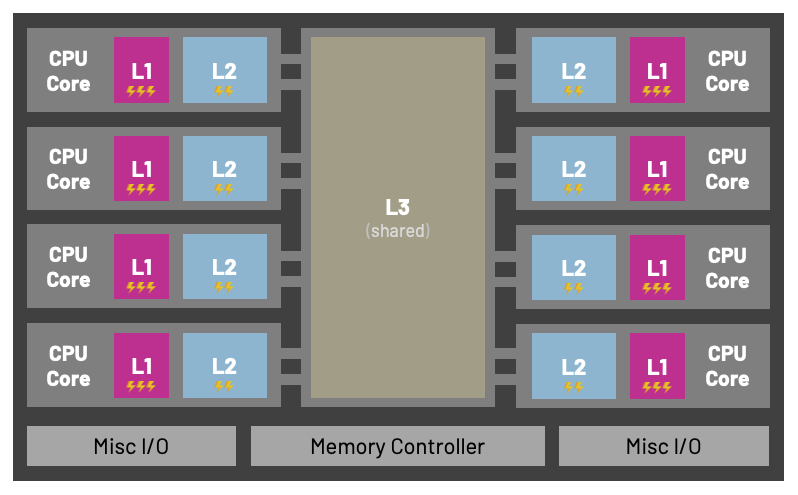
Below you can see an example of a multi-core CPU architecture that contains L1, L2, and a shared L3 cache. The Nehalem microarchitecture was used in the first generation of Intel Core i5 and i7 processors.

Data Cache & Instruction Cache
Another aspect that we must mention is that most computers have a dedicated cache for instructions (i-cache) and another cache for data (d-cache). As one would expect, instruction cache constains program instructions, while data cache contains data. Instruction cache will store the assembly/opcode instructions and data cache will store the data accessed from main memory.
The reason for this separation has to do with the nature of what we are accessing and how we expect the data to be accessed. One major difference between them is that data cache must be capable of performing both read & write operations, while instruction cache needs to provide only read operation. There is also some expectations in terms of how we assume data & instructions data to be accessed (sequentially or randomly).
Just to add some context, if you took Gustavo's PlayStation Programming course, you know that the PS1 had only 4 KB of instruction cache and it did not have a proper data cache. Writing PS1 code that efficiently takes advantage of the i-cache was a challenge but it was often required to make games run smoothly.
The Scratchpad: Most MIPS processors have a data cache, but the PlayStation did not implement a proper d-cache. Instead, Sony assigned 1 KB of fast-SRAM that most developers refer to as the "Scratchpad." On the PS1, the Scratchpad is mapped to a fixed address in memory and its purpose is to have a more flexible "cache system" available to the programmer.
Modern architectures also have separate caches for instruction & data. Most ARM CPUs have a separate I and D cache inside L1, but are combined inside L2.
Even Apple Silicon M1 and M2 chips have separate instruction & data caches. The M2 high-performance cores have 192 KB of L1 instruction cache, 128 KB of L1 data cache, and share a 16 MB L2 cache, while the energy-efficient cores have a 128 KB L1 instruction cache, 64 KB L1 data cache, and a shared 4 MB L2 cache.
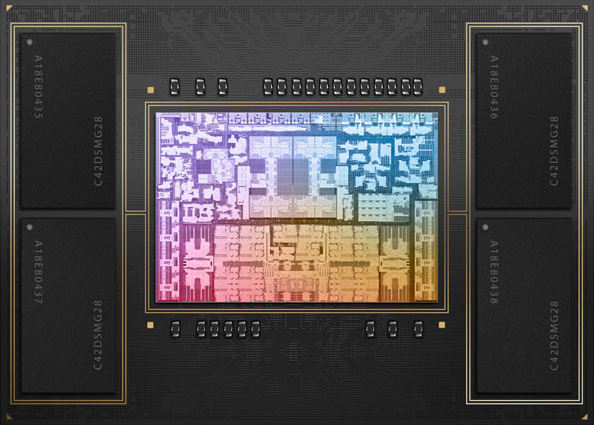
Invoking the sysctl command in my laptop running on top of an Apple Silicon M2 Pro, we can see the values of L1 and L2 cache sizes:
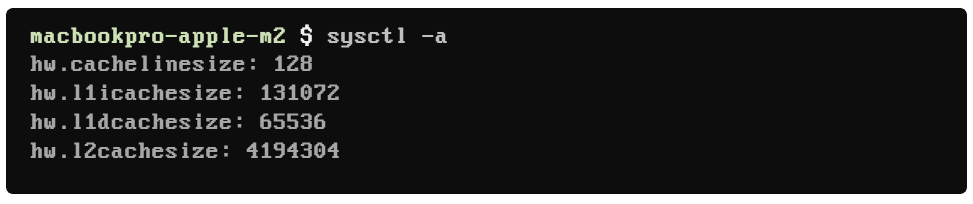
Executing the same command in my older MacBook Pro running on an Intel Core i9, I get different values for L1, L2, and L3 cache sizes:
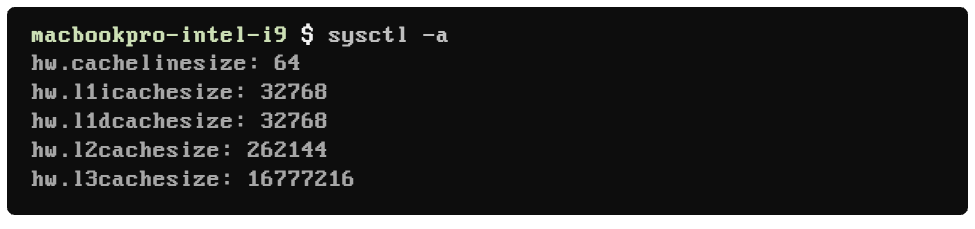
Do you see how we have different sizes for instruction and data cache in L1's icachesize and dcachesize?
Where to put data in cache?
There are many cache placement policies. Some popular examples of popular placement policies are direct-mapped cache, fully associative cache, set associative cache, two-way skewed associative cache, and pseudo-associative cache.
A direct-mapped cache is the simplest approach, where each memory address maps to exactly one cache block. The cache is organized into multiple sets with a single cache line per set.
Since this aims to be a beginner-friendly article, let's simplify things and only cover direct-mapped cache. Below is a very simple example of a 16-byte memory and a 4-byte cache (four 1-byte blocks).
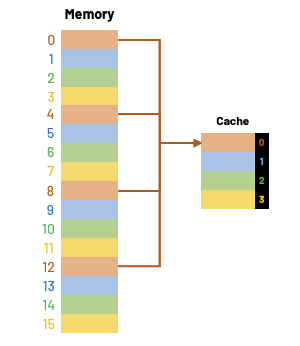
- Memory locations 0, 4, 8, and 12 all map to cache block 0.
- Memory locations 1, 5, 9, and 13 all map to cache block 1.
- Memory locations 2, 6, 10, and 14 all map to cache block 2.
- Memory locations 3, 7, 11, and 15 all map to cache block 3.
How do we compute this mapping?
One way of finding out which cache block a particular memory address should go is by using the remainder operator. If the cache contains \(2^k\) blocks, then the data at memory address i would go to cache block index:
For example, using a 4-block cache, memory address 14 would map to cache block 2.
This mod operation is easy to do with a computer, as it is equivalent to masking at the least significant bits of the memory location. Given that our cache is 4 bytes long, we look at the last significant \(k\) bits of the address.
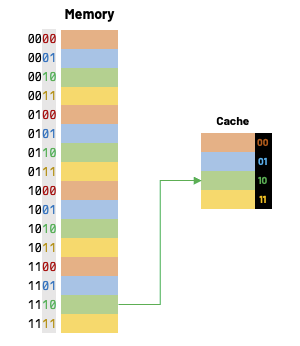
How do we find data in cache?
I hope it's clear that our cache block index 1 could contain data from addresses 1, 5, 9 or 13. Of course, this logic holds true for all other cache blocks, so the question really becomes "how can we distinguish between these potential addresses that all map to the same cache block index?"
One approach to solve this is to add tags to the cache. These tags supply the rest of the address bits to let us distinguish between different memory locations that map to the same cache block.
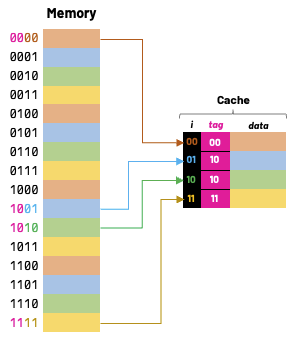
Valid Bit: One final information that we also store in cache is a valid bit. As we start, the cache is empty and all valid bits are set to zero. When data is loaded into a particular cache block, the corresponding valid bit flag is set to 1.
I also hope it's clear to everyone by now that the cache does not contain just raw copies of data in memory; it also holds metadata and extra bits to help us find data within the cache and verify its validity.
Coding with cache in mind
As programmers, it is important that we write code that is cache-friendly. Properly using the cache of our computer or game console can really affect the performance of our software. Especially in modern machines that were designed with multiple cores and large cache sizes.
Let's look at a couple of extremely simple examples and try to understand what is going on in terms of cache access.
Example 1: Cache locality
We should keep most of our data in contiguous memory locations. That way, when our code sends the first access request, most of the data that will be used will get cached. This is closely related to our choices of data structures.
We are trying to keep:
- Good temporal locality: aim for repeated references.
- Good spacial locality: aim for stride-1 references.
As an example, think of two functions that loop all entries of a matrix summing the elements. A cache-friendly code should respect the stride-1 pattern of the matrix.
Our first function loops all rows and iterates all nested columns of that row one by one:
int sum_matrix_rows(int mat[M][N]) {
int sum = 0;
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
sum += mat[i][j];
}
}
return sum;
}The second function flips the access, looping all the columns of the matrix first and nesting the loop of rows inside:
int sum_matrix_rows(int mat[M][N]) {
int sum = 0;
for (int j = 0; j < N; j++) {
for (int i = 0; i < M; i++) {
sum += mat[i][j];
}
}
return sum;
}To understand why the first function is better from the perspective of data locality, we must recall that C arrays are allocated in row-major order. In other words, each row is contiguous in memory.
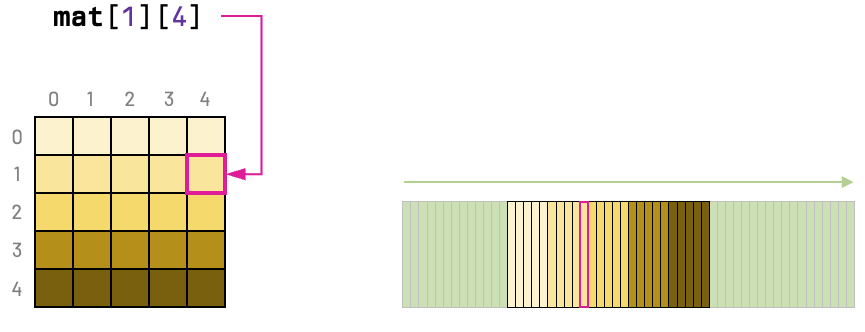
If we consider a small-enough cache size, we'll have considerably more cache hits with the first function.
Linked lists: The data locality argument is also why linked lists have a bad reputation nowadays. Looking at them from a data-oriented-design perspective, linked items can be all over the memory and that is an invitation for cache misses.
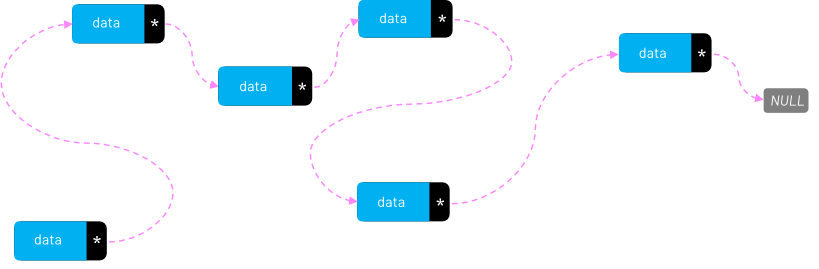
Example 2: Avoid complex loops
To make the code cache friendly, it is recommended to avoid using large loops. Instead, we should break a large loop into smaller ones. The reason for that is that if the loop's body needs to access a lot of data, the cached items at the beginning of an iteration can "drop out" from the cache by the iteration's end. Afterward, when the flow gets back to the beginning of the next iteration, there will be a cache miss.
Example 3: Struct alignment
Making the size of each object in memory smaller can help us improve cache use.
Structs in C are a very useful way of packing variables into one big chunk of memory, but they have their own special way of allocating memory. If you're new to C, you'd be surprised to know that we can be "wasting" memory when we declare our structs.
In C and C++, every data type has a size; it may be 8 bits, 16 bits, etc. So, if structs are agglomerations of these data types, you may deduce that structs will have the size of all the its types added up, and that is surprisingly incorrect if your struct has has different types inside.
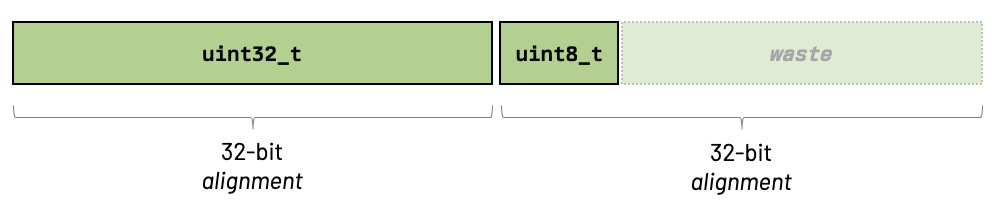
The reason for that is because structs have a natural alignment, which is the size of their largest member. Therefore, if you have a struct that has two members: a 32-bit one and a 8-bit one, the alignment will be the size of the greatest value: 32 bits. In this case, the total memory consumed by this struct is 64 bits!
struct {
uint32_t a;
uint8_t b;
}
Let's look at another example where our struct has more than two members:
struct {
uint16_t a;
uint32_t b;
uint16_t c;
}Since the largest member is 32 bits, we know that the alignment of our struct is 32 bits. Observe how this alignment plays a direct role in the size of the struct in memory:

Pay attention to how the struct's alignment required a padding between the first and the second members and another padding at the end (to fill the alignment).
We could improve things by re-ordering our struct members. Look at what happens if we change the order of the second and third members:
struct {
uint16_t a;
uint16_t b;
uint32_t c;
}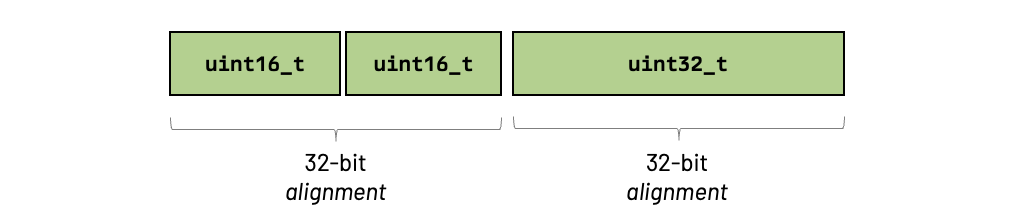
We reduced the size of our struct just by playing with the alignment and the order of members. The take here is that making things occupy less space in memory can help us better fit data in our cache lines and, by doing so, reduce cache misses.
You'll see some programmers also solving this by simply dividing the data. To avoid memory leaks and cache misses if the data gets larger, we can store these as separate values instead of bundling them inside a single struct. So if we want to have multiple instances of a struct, we just treat them as two separate arrays of the same size.
int size = 100;
uint8_t *a = malloc(size * sizeof(uint8_t));
uint8_t *b = malloc(size * sizeof(uint8_t));Example 4: Compiler flags
Compilers are super smart nowadays, so we can help them by setting the correct compiler flags for our project. Some examples of compiler optimizations include unrolling loops, optimizing function calls, vectorization, and padding data structures.
Wrapping things up
With our new knowledge of how computer memory works and how it works along with the CPU, I wish you most of luck to dive deeper in cache manipulation.
As I mentioned, these are extremely simple examples but the ideas that they demonstrate underpin the basics of how cache works.
Where to go from here?
You can start with the basics, like coding simple programs and try to benchmark them; organize the structs and do them the best as you can! You can also refactor your code to make it faster. It's all evolution from here!
If you liked this blog post, you can follow me on X/Twitter @lemmtopia. :)
Have fun!


